[일반물리학개념] 연속방정식

연속방정식과 관련된 실생활

왼쪽은 호스를 들고만 있고, 오른쪽은 호스 끝부분을 누르고 있다.

그림이 좀 이상하지만, 물이 나오는 호스입니다.

왼쪽은 호스를 가만히 들고 있는 모습이고, 오른쪽은 호스의 끝부분을 누르는 모습입니다.

일상생활에서 이런 장난을 많이 치지 않습니까? 호스의 끝부분을 누르면 물이 엄청난 속력으로 나갑니다.

이것을 이용하여 다른 사람을 공격할 수 있습니다.

 

이것을 분석해봅시다.

호스 끝을 누르는 것과 물의 속력은 무슨 관계가 있을까요?

가만히 생각해보면, 물이 흐르는 호스의 단면적이 좁아지면 물의 속력이 빨라집니다.

즉 물의 속력은 호스의 단면적과 관련이 있는겁니다.

 

또한 유체는 너무 어렵기 때문에, 다루기 쉬운 이상 유체를 대상으로 분석해보겠습니다.

지난 글에 따르면 이상유체는 "비압축성"이란 특징이 있습니다.

https://saeutang.tistory.com/10

[일반물리개념] 이상유체의 운동: 이상유체의 성질 (비압축성 유체 등)

비압축성으로 인해, 어떤 관에서 흐르는 유체의 (시간당)부피흐름은 일정하게 됩니다. (단면적이 변해도 찌그러지지 않는다)

이를 수학적으로 생각해볼까요?

 

 

연속방정식의 수학적 표현

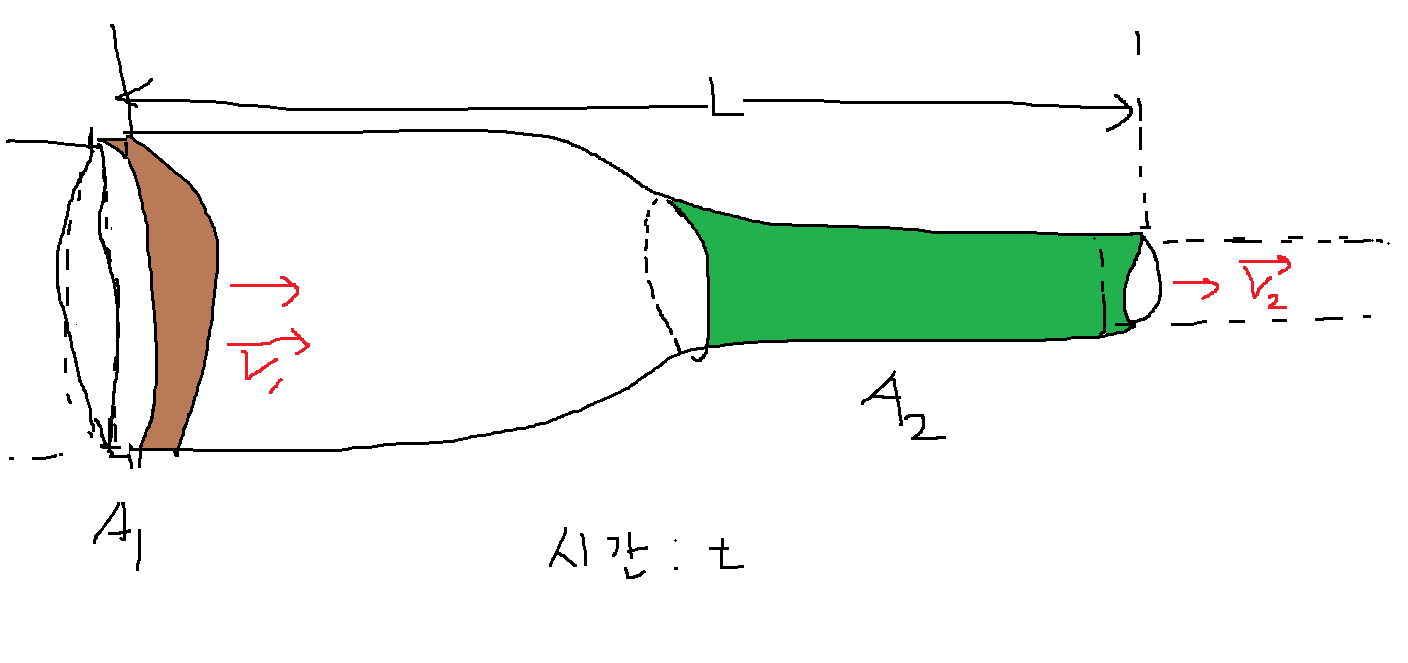
단면적이 변하는 관을 지나는 유체

위 이상한 그림을 보면, 길이가 L인 관을 유체가 왼쪽에서 오른쪽으로 흐르고 있습니다. 또한 관의 단면적이 왼쪽은 A1, 오른쪽은 A2로 다른 상황입니다. 속력은 왼쪽에서 v1, 오른쪽에서 v2인 상황입니다.

 

여기서 비압축성으로 인해 왜 부피흐름이 동일한지 추가설명을 하겠습니다.

단위시간이 흐를 때마다( $\triangle t$ 라고 하죠),

왼쪽에서 $\triangle v$ 만큼의 유체가 들어올 겁니다.

그런데 이상유체는 비압축성(찌그러지지 않음)이기 때문에,

들어온 만큼의 유체($\triangle v$)에 밀려

$\triangle v$ 만큼의 유체가 나갈수 밖에 없습니다.

그렇기에 들어온 만큼 나가는 것이죠.

자 이제 이 상황을 수학적으로 표현해보겠습니다.

관계식을 하나 유도할 것인데, 우리가 호스에서 발견한 관계는 단면적과 속도의 관계입니다.

또한, 시간당 부피흐름이 일정하다는 것을 발견했습니다.

 

유체를 이루는 한 입자의 속력이 v라고 한다면, 시간 $\triangle t$ 가 지나는 동안 입자는 $\triangle x$=v$\triangle t$ 만큼의 거리를 움직입니다. 

그렇다면, 이때 움직인 유체의 부피는 $\triangle v$=A$\triangle x$=Av$\triangle t$가 됩니다.

단면적이 변하는 관을 지나는 유체

이를 이 그림의 왼쪽, 오른쪽에 적용하면 다음과 같습니다.

 

$$ \Delta V= A_{1}v_{1} \Delta t= A_{2}v_{2} \Delta t$$

즉 $$A_{1}v_{1}=A_{2}v_{2} (연속방정식)$$ 입니다.

 

바로 이게 연속방정식입니다. 속력과 단면적 사이의 관계식을 이상유체의 흐름에 대한 연속방정식이라 합니다.

 

 

연속방정식의 의미?

그런데 이게 무슨 의미가 있냐고 할 수 있습니다.

연속방정식은 보존법칙을 표현한 거라고 보시면 됩니다. 

유체의 양이 변하지 않고 특정 구간에서 구간으로 흐를 때의 상황을 식으로 표현했습니다.

즉 유체에서의 보존법칙을 표현한 식이라고 보면 됩니다.

 

 

다음엔 베르누이 방정식에 대해서 알아보겠습니다.